Abstract
The typical viral model defines active marketing users to maximize social networks accepting a product, including unlimited users, campaign budgets and time. In fact, there is a need for different advertising campaigns that show users of limited interest; users are convinced to spend costs, advertisers limit their budgets and expect their adoption to be maximized within a short period. Considering a user’s problem, money and restrictions, we have met the challenge as the problem to optimize AL modular in a continuous time diffusion model at the intersection of the Metroid and multiple backpack constraints. E | | + N | V, n = 0 (1 / ε2) randomization and influence user evaluation algorithm randomizing network estimation with ribs (| V | nodes, | e) values O (n | | | as subprogram we developed algorithm with a portal-aggressive algorithm with for adaptation k backrest coefficient borders to best approach / (2k + 2) using the algorithm to estimate the effect. Comprehensive millions of experimental network nodes show that the proposed algorithms provide the technologies and Latest regarding efficiency and scalability.
Introduction
Online social networks play an important role in promoting new products, disseminating news, success in political campaigns and the dissemination of technological innovation. In this regard, the problem of maximizing the effect (or viral marketing problems) is usually the following flavors: the social of each other in the network to determine the user effectively convincing the product, that will affect other users on the network and take maximum obese. This problem has been widely studied in literature and algorithms. Usually, this is represented by one product (e.g., an online social platform) which is endlessly interested in the user, an unlimited budget and infinite time. However, in fact, the host usually tends to be more severe:
• Different restrictions on the section. Some products can be distributed at the same time as the same set of social things. These products can have different characteristics, such as income and speed of spread.
• Time limits: advertisers are expected to take action at a certain time interval, and different products may have a different timescale.
Influence Estimation
Gomez-Rodriguez et al. Developed a model of continuous diffusion. (2011), and then expressly thinks the problem is to assess the problem regarding probabilistic graphics models. Given that efficiently efficient impact values for each node are very insignificant, we are developing a scalable algorithm for the predictions of the effects that millions of network nodes can deal with. The procedure for estimating the impact forecast as an important construction block for our maximum algorithm will be followed.
Networks of continuous differences
A constant density diffusion model associates time along the edge of the transmission along the border, unlike previous models, a specific time, with each side combined with the function of transferring, that is, E., and the possibility of continuous infection of each rib. Also, at the same time, time-consuming models differ in the sense that the events are in the following case that are repeatedly produced in shells, but the time of the events is generated directly from the function to translate in continuous time models.
Continuous independent cascade model. Thinking of the targeted web, G = (V, E), we use a separate cascade model to shape the spreading process. The process starts with a series of contaminated source nodes (A), which initially found the unique contamination (idea, nozzle or product) as zero. Pollution is directly transmitted to neighbors with output edges from welded seeds. The transition requires each side of random waiting time (τ), taken from different independent double times (one at each end). Then, the infected neighbors offer the infection of their neighbors, and the process continues. We assume that the infected node is infected for each diffusion process. So, if the site is contaminated with some neighbors, it will be just a neighbor, a birth parent, in which the unit is infected first. As a result, all of the processes of non-imperative steering graph (SCM) is induced, although the network can be randomly targeted network.
Suitable conduct functions. It is for directional tubes (j → i) conditional node density that is infected at time t | formal Dwarf communication function fji (tj TI). If it is accepted that the variable change is: fji (ti | tj) = fji (τji), where τji: = ti – tj and causative: τji <0 mura fji (τji) = 0. The Its functions include parameter, such as exponential and Rayleigh functions, and use and predict non-parametric functions from cascading data.
Overall Algorithm
Algorithms are to optimize low modular backpack with different constraints to achieve coefficients about 1 – 1. Therefore, we can tempt
- Equation (19) and | V | Backpack
- Borders, the problem, therefore L | a problem of submodular optimization. +
- | V | blocking. However, this naive approach does not fit for large-scale
- Cases, since the length of these algorithms,
- blocking. Instead, we prefer algorithms for lower modular optimization
- k on the backpack and borders of matroid P, gets the best ratio
This is the 1 with polynomial time algorithms. However, P + 2k + 1 is still not enough, since our problem is k = | L | P = 1 can be small, but it can be great.
Here, we developed an algorithm to obtain best rate approximation, using the following important comments regarding the structure of the tasks defined in the equation (19): Restrictions of a backpack on Zi * different groups Full sets of tires, and the purpose – the functions size by the different groups,
Details of the BudgetMax algorithm defined in Algorithms 1. BudgetMax different values of the threshold values of the ρ density and subroutine start to get answers for each ρ. Special product for a specific user and, ultimately, a solution with the maximum value of purpose. Amazingly, the algorithm offers a limit to the search area for a set of optimum costs. Subroutine data for permanent solutions of ρ is to determine the intensity threshold explained in the Algorithm 2. Geometrically Inspired algorithm dimensions in the ratio of 1 + factor as far as the set (G) and the gain limit threshold (wt) It will not be enough They can be set identical to zero from the lazy evaluation intuition (Leskovec et al., 2007). In each wt, the sub-section selects all new elements that provide the following properties:
1. This can be done, and the density coefficient (the ratio of the limiting gain and the cost) exceeds the current density threshold;
2. Edge increase
f (G | G): = f (G ∪ {z}) – f (G) above the yield threshold threshold.
The term “density” is used based on the knapsack problem where the marginal returns are by weight and volumevolume. High intensity means earning a lot without paying enough money. Soon, the algorithm does not take into account high-quality tasks and chooses what is possible repeatedly with a small victory too much.
Experiments on synthetic and real data
In this section, we assess the accuracy of the anticipated effect provided by ConTanEst and then examine the effectiveness of increasing the impact on artificial and real networks, including a contest in the context of BudgetMax. Our approach shows that the quality of both speeds and solutions is better than the most modern modes.
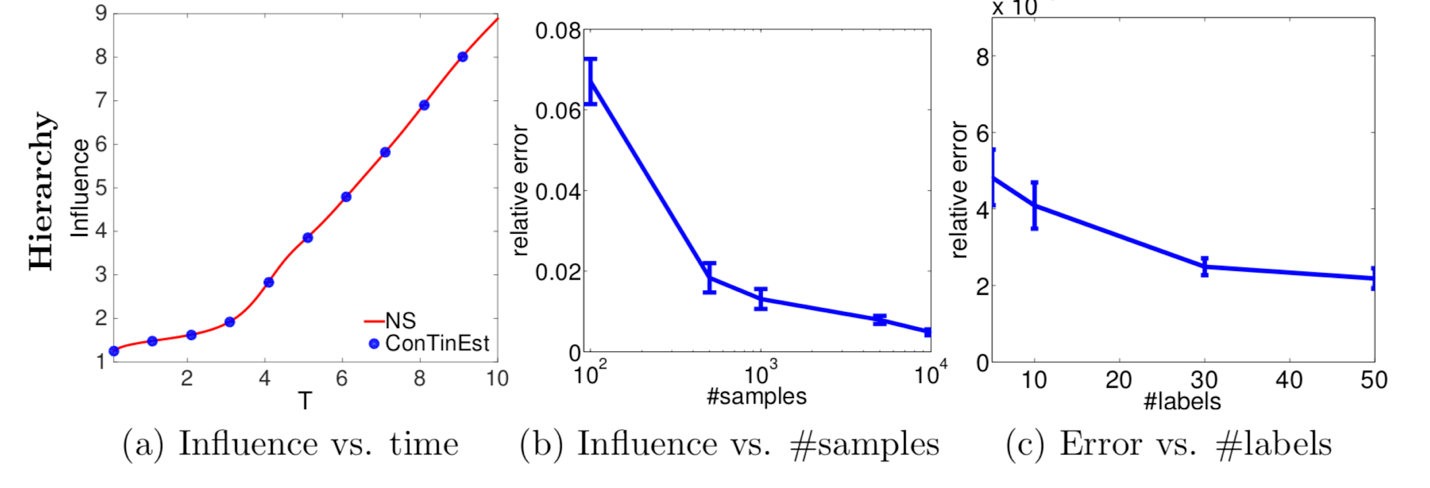
Core-environment forecast, random, and forecast for hierarchical networks with 1,024 nodes and 2,048 fronts. Column (a) shows the estimated effect of NS (close to the predicted reality) and continues to increase the time window, T; Column (b) shows the relative error of ConTinEst with respect to sample number 5, randomly marked and T = 10; Column (c) shows the relative error of ConTinEst with respect to 10,000 random samples and the number of random tags with T = 10.
Adaptive threshold effects
We have investigated the accuracy of the algorithm of the threshold adaptive value and the influence over time of the algorithm investigation concerning the lazy evaluation method. Note that the execution of the slow evaluation and the duration of the work do not depend on δ since it is not related to it. Panel (a) shows the threshold effect. As expected, the higher the value of δ, the lower the precision. However, our method is relatively robust for a particular choice, since its performance is always above 90% relative accuracy even in large dimensions. Panel (b) shows the execution time from the thresholdthreshold. In this case, the higher the value, the shorter the work time. In other words, the study confirms the perception that the period and the distribution can shift the quality of the solution to δ.
scalability
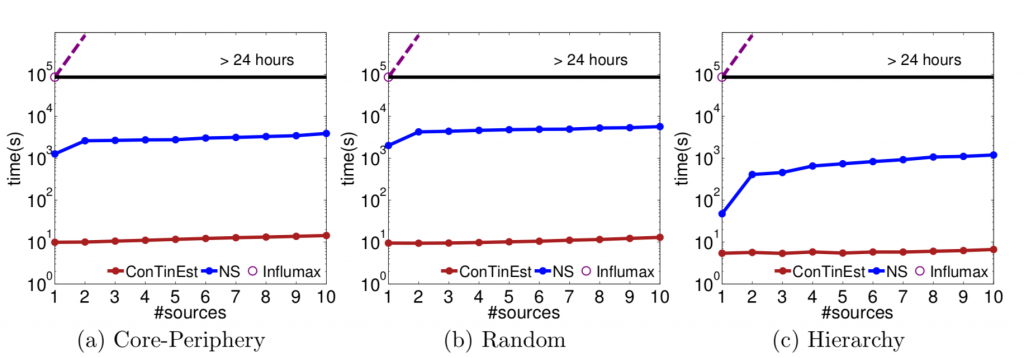
In this section, we begin with an assessment of the scalability of the proposed algorithms concerning the classic maximization problem. We only have one product with the main flow restrictions for our users. It is comparable to Influmax and Naive Sampling (NS), which is the most modern method for continuous assessment of time and maximizing working time. For ConTinEst, we make 10,000 samples in the outer loop, each of which contains five random tags in the inner loop. We attach ConTinEst as a subroutine to the standard greedy algorithm. We also recruit 10,000 samples for NS. The first two experiments were performed with a single 2.4 GHz processor.
Experiments on Data
In this part, we first decide how well our proposed algorithm reflects the true impact on a series of global data. We will then evaluate the quality of the resources chosen to maximize the effect of different constraints. We used a set of MemeTracker public data with over 172 million news articles and blog posts from 1 million significant sites and blogs.
Conclusion
We studied the effect of evaluation questions and maximizing the continuous-time diffusion model. First of all, we recommend ConTinEst, a randomization algorithm to estimate the efficiency of scale up to millions of nodes, thus greatly improving the accuracy of the forecast regarding accuracy than previous methods. When we are in a routine to the productive impact of large networks, our goal is to optimize the impact of different types of products (or information) in the time of their distribution networks based on different practical constraints: Different products can be diffused differently; In a specific time window, the effect is only considered; For each user that can be encouraged to just a small number of products, and all budget products are limited to the campaign, which is expensive to deploy to the user. We are creating a new formulation to maximize at the matrix crossing restrictions and group feedback boundaries, and then we develop an adaptive greedy algorithm portal, which we call Bud-getMax, which is useful in guaranteeing a reasonably priced approach. Experimental results show that the proposed algorithm is better than the other scalable option of its synthetic and accurate data set. There are some interesting open problems. For example, when the effect is evaluated using ConTinEst, its error is a random one. How does this affect the function of the module? Is there an optimization algorithm with greater accuracy for random error? These issues are reserved for future work.
References
Odd Aalen, Oernulf Borgan, and H ̊akon K Gjessing. Survival and event history analysis: a process point of view. Springer, 2008.
Ashwinkumar Badanidiyuru and Jan Vondra ́ak. Fast algorithms for maximizing submodular functions. In SODA. SIAM, 2014.
Eytan Bakshy, Jake M. Hofman, Winter A. Mason, and Duncan J. Watts. Everyone’s an influencer: Quantifying influence on Twitter. In International Conference on Web Search and Data Mining (WSDM), pages 65–74, 2011.
Christian Borgs, Michael Brautbar, Jennifer Chayes, and Brendan Lucier. Influence maximization in social networks: Towards an optimal algorithmic solution. arXiv preprint arXiv:1212.0884, 2012.
Wei Chen, Yajun Wang, and Siyu Yang. Efficient influence maximization in social networks. In Knowledge Discovery and Data Mining (SIGKDD), pages 199–208. ACM, 2009.
Wei Chen, Chi Wang, and Yajun Wang. Scalable influence maximization for prevalent viral marketing in large-scale social networks. In Knowledge Discovery and Data Mining (SIGKDD), pages 1029–1038. ACM, 2010a.
Wei Chen, Yifei Yuan, and Li Zhang. Scalable influence maximization in social networks under the linear threshold model. In International Conference on Data Mining series (ICDM), pages 88–97. IEEE, 2010b.
Wei Chen, Alex Collins, Rachel Cummings, Te Ke, Zhenming Liu, David Rincon, Xiaorui Sun, Yajun Wang, Wei Wei, and Yifei Yuan. Influence maximization in social networks when negative opinions may emerge and propagate. In SIAM International Conference on Data Mining (SDM), pages 379–390. SIAM, 2011.
Wei Chen, Wei Lu, and Ning Zhang. Time-critical influence maximization in social networks with the time-delayed diffusion process. In AAAI Conference on Artificial Intelligence (AAAI), 2012.
Aaron Clauset, Cristopher Moore, and M.E.J. Newman. Hierarchical structure and the prediction of missing links in networks. Nature, 453(7191):98–101, 2008.