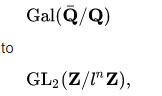Prevalence of Obesity in USA

Introduction

If one talks about the number theory, the Fermat’s Last Theorem which is at times also known as the Fermat’s conjecture that there are no positive integers (Krantz and Parks, 2014). That can make sure that the a, b and c that is going to satisfy the equation an + bn = c specially if there is a case when the value of the integer is greater than 2 (Cornell et al. 2013). The cases where n =1 or n =2 does seem to have many solutions that are going to be pertaining to the overall antiquity of the equation (Cornell et al. 2013). The first time when the Fermat’s Last Theorem was conjectured was in the Sirre de Fermat during the course of the early 16^th century and was witnessed in the margin of a copy of the Arithmetical (Cornell et al. 2013). In this conjecture the placement of the proof that was too large to be fitting into the margin (Cornell et al. 2013). The first successful proof of the conjecture was released in 1994 and was being done by Andre Wiles. It took about 358 years of the effort by the mathematics expert (de Fermat et al. 2001). In this paper, it would be seen what is the relevance of Fermat’s Last Theorem, what is the background of Fermat and why the solving of this theorem is considered as one of the major breakthrough in the mathematics (Cornell et al. 2013).

Background of the Pierre de Fermat

Fermat was born during the course of the early 17^th century. He was originally from Gascony, where his father was a well known leather merchant (Cornell et al. 2013). On the other hand, his mother’s name was Claire de Long. Pierre had one brother and couple of sisters and as far as the evidence of this earlier education is concerned, even though it is not much known but there are certain sources that point that he has received his early education at the College de Navarre (de Fermat et al. 2001).

Fermat’s Refusal to Publish his Work

There was a strange thing about Fermat that stopped him from publishing his work (de Fermat et al. 2001). As a matter of fact, some of this friends were fearing about the fact that all of his contributions and work is going to be forgotten soon if there is nothing that is done about it (Cornell et al. 2013). It was his son Samuel that took the task of making sure that he collects all the work that is carried out by Fermat (Cornell et al. 2013). Gigantic effort was carried out by his son to make sure that he gets to collect all the work that is done by Fermat as well as making sure that collection of all the mathematical papers is being done by him (Cornell et al. 2013). There were numerous comments that were written as a form of notes in the books (Cornell et al. 2013). Samuels made sure that he gets to publish all the work that is being done by his father. It was during this effort that the infamous last theorem emerged and was published. The way it was found is also interesting as Samuel wrote about the whole thing as a form of the note in the copy of his father’s manuscript (Stewart and Tall, 2001).

Subsequent Development and Efforts about the Solution about the Theorem

With the special case when n = 4, it was proved by Fermat himself. What it does is that it just about suffices the whole point of the theorem for the exponents of the n that are prime numbers (Cornell et al. 2013). It has to be noted that this direction is at times considered to be trivial to be proven completely at each and every level. During the course of the next two centuries, the conjecture was proven for only two prime numbers which were 3, 5 and 7. It has to be noted that Sophie Germaine innovated and provided an approach when it comes to the relevant classes of the primes and narratives (de Fermat et al. 2001). In the middle of the 19^th century, there was an extension into the premises of the theorem when Ernst Kummer extended the whole premises of theorem for all the regular primes that are carried out for the given time period (Cornell et al. 2013). The idea that was given by Ernst Kummer was to make sure that the leaving out all the irregular primes is needed to be done and the exercise is needed to be carried out at the individual level (Cornell et al. 2013). Further building on the work done by Kummer, as well as making use of the computational studies, the other mathematics expert were able to make sure that all the prime exponents up to four million were being provided (de Fermat et al. 2001). The problem with this approach though was that more or less all the exponents were inaccessible to be proven (Brown and Freedman, 1990). The inaccessible proof in mathematics mean that the all the mathematics deem the proof to be impossible (Brown and Freedman, 1990).

Pierre de Fermat

Pierre de Fermat was the French lawyer and mathematician. One of the earliest proof of his greatness is the fact that he is given lot of credit for the early development of the infinitesimal calculus (Cornell et al. 2013). The other technique that was being used by him was of the adequality which later on played a major part in the advancement of the mathematics as a subject (Cornell et al. 2013). But for the thing that is generally regarded and well knows are that discovery and the method of finding the largest and the smallest ordinates of the curved lines (Brown and Freedman, 1990). These lines are analogous to the way differential calculus is being carried out. Later on this research was witnessed in some of the other number theories (Jones et al, 1998). Not only that, he is also credited for the introduction of the Fermat’s principle that was used for the light propagation for a long period of time (Brown and Freedman, 1990).

Overview of the Theorem

If one looks at the overview and the overall history of the theorem, one has to actually have an understanding of the Pythagorean origins (de Fermat et al. 2001). The equation that goes something like this:

x² + y² = z²,

This equation as the number of positive integer solutions for all the corresponding variables. These solutions are well known as the Pythagorean triples (de Fermat et al. 2001). Now, in 1637 write in the margin of the book about the more generalist version of the equation that was:

aⁿ + bⁿ = cⁿ

This equation had no positive integers if the value of the n as an integer is greater than 2. He claimed that he had known the proof for this general conjecture (Cornell et al. 2013). The key aspect that is needed to be noted here is that there was no proof for this conjecture. As a matter of fact, there are large numbers of people who claim the fact that no proof about this whole equation was ever being found (Cornell et al. 2013). The interesting part is that his claim was discovered about three decades after his death (Brown and Freedman, 1990). This was the claim that was later on known as Fermat’s Last Theorem, and it was three and a half centuries before this eventual solution about this claim was being reached on. The claim became one of the most well known and unsolved problem of the mathematics (GROOS et al. 2016). There were many attempts that were carried out to make sure that the prompt solution of the theorem can be found out (Cornell et al. 2013). There were many attempts carried out to make sure that the substantial development of the theory (Cornell et al. 2013), The claim and theorem became well known as one of the basic problems whenever there was discussion about the number theory (Brown and Freedman, 1990).

Pythagoras and the Diaphanous

If one looks at the ancient times, it can be seen that the Pythagoras theorem was the one that can closely related to this theorem (Brown and Freedman, 1990). The idea is that the triangle whose sides that were supposedly arranged in the ratio 3:4:5 is likely to have a right angle as one of its angles (Cornell et al. 2013). It was used mainly in the construction of the whole premises as well as its usage was also seen in the geometry as well. In the ancient times, there was another discovery that pointed out towards the fact that how there is going to be just one example and rule that any triangle where the length of the sides are squared when they are added together, (32 + 42 = 9 + 16 = 25) is going to be equal to the third side of the squared. It is also going to be shaped in the method of the right angle triangle (Cornell et al. 2013). What Fermat’s Last Theorem used to do is that how it used to look at this equation in the manner that for the powers that are other than 2, there is a strong likelihood that the many triples are going to be used in solving the equation (Brown and Freedman, 1990). The equation is going to be solved for n + .2. In this case there is no solution other than the trivial solution x = y = z = 0 exists when the exponent of the 2 is replaced by any larger integer to say the least (Brown and Freedman, 1990).

Statements that Equate the Theorem

If one talks about the range of the alternatives that are going to stand in terms of the development of the equation, the key thing that is needed to be noted here is that how the mathematical equivalent are going to be there for the original statement of the problem (Brown and Freedman, 1990). To make sure that they are stated in the correct manner, the mathematical notation (Brown and Freedman, 1990). Now, letting the N be the set of the natural numbers such as 1, 2, 3, and Z being the set of the integers such as 0, ±1, ±2, Letting Q be the set of the rational numbers (Brown and Freedman, 1990) a/b where a and b are in Z with b≠0. The subsequent solution that is going to be followed in this case is going to be written in the form of xⁿ + yⁿ = z^n. The key thing that is needed to be noted here is that how x, y and Z are going to be zero or trivial solution (Darmon et al. 1995). To make sure that the comparison is being carried out in the right manner, it would be a good idea to start with the original formulation (Cornell et al. 2013). The original statement that is related to the theorem is about the fact that how with the n, x, y, z ∈ N (this implies that how all the set of the positive numbers are going to be followed into the whole number (Cornell et al. 2013). In these cases, n > 2 and the equation are going to be  xⁿ + yⁿ = z is not going to be having any solution to say the least. In the same context, the equivalent statement is going to be written in the format, xⁿ + yⁿ = zⁿ,  where the integer is either going to be 3 or equal to be 3 and there is not going to be any non trivial solutions for the solutions x, y, z ∈ Z,

Wile’s Proof of the Fermat’ Last Theorem

Now, coming towards the subsequent solution and the proof of the last theorem, and the proof of this theorem is being credited to Andrew Wiles (Cornell et al. 2013). It is about the space case of the modularity theorem that is related to the elliptic curves (Darmon and Merel, 1997). Being looked together along with the theorem that was given Ribet, the solution is going to provide a proof regarding the way Fermat’s last theorem (Brown and Freedman, 1990). Looking at the way theorem works, the idea is that how the modularity theorem is going to work out and how at times they are universally considered inaccessible to the proof by all the major mathematics expert (Cornell et al. 2013). The solution and the proof of the theorem is considered as a major achievement in the mathematics history due to the fact that it was considered to be almost impossible to proof the theorem with the existing knowledge to say the least (Brown and Freedman, 1990).

Techniques Used by Wile While Proving Theorem

There were many techniques used by Wiley during the course of the fact that how this whole theorem was being proved (Brown and Freedman, 1990). The techniques related to the algebraic geometry and number theory was the ones that were extensively used along with some other ramifications related to the branch of the mathematics (Cornell et al. 2013). Not only that, it also uses the standard constructions related to the way modern algebraic theory is going to be working out (GROOS et al. 2016). The category of the schemes and the Iwasam theory was also witnessed during the course of the whole time period (Brown and Freedman, 1990). Looking at the manuscript of the proof, it is about 129 pages document (Cornell et al. 2013). The construction of the proof took about seven years for Wile and he had to dedicate considerable research time during the course of the whole event (Adleman and Heath-Brown, 1985). As soon as the proof was being done, it was regarded as one of the major achievements in the number theory (Adleman and Heath-Brown, 1985). The path that was taken by Wile to prove the theorem was based on the fact that how the modularity theorem was being taken care off. There was a special case of the semi stable elliptic curve was being formulated (Adleman and Heath-Brown, 1985). At the same time, the proof also made sure of the modularity lifting techniques as well as opening entirely new approaches that are related to hosts of other problems that were witnessed in the same time period (GROOS et al. 2016). Due to making sure that the solution of the Fermat’s Last Theorem was being solved, he was knighted (GROOS et al. 2016).

Mathematical Detail of the Proof Provide by Wile

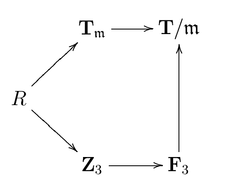
While proving the theorem , the attempt was made by Wiles to make sure that the elliptic curves so that the countable set of modular forms are being used (Cornell et al. 2013). He was able to found the fact that how the direct approach is not going to work in the case of this theorem (GROOS et al. 2016). Wiles denoted the more specific ring homomorphism which was denoted as something like this (Brown and Freedman, 1990).

Wiles had decent insight about the fact that in most of the case regarding the ring homomorphism, there is a likelihood for the ring isomorphism (Cornell et al. 2013). There was also a realization on his part that the map that exists between R and T is an isomorphism (GROOS et al. 2016). This phenomenon is called as numerical criterion (Brown and Freedman, 1990). When this result was given, the whole premises of the Last theorem are reduced to the statement that the two groups are going to have the same order (Cornell et al. 2013). Wiles was able to define four cases with the flat deformation and each of the case required more effort and time on the part of the user to prove that how they are treated in the separate article that is witnessed in the same volume for the entitlement of the Ring theoretic properties that are witnessed in the Hecke algebra’s (Brown and Freedman, 1990).

General Approach and Strategy

Given an elliptic curve that exists over the E field over the Q of the rational numbers E(Q) for every prime power.

In this case, it can be seen that how the invertible that are linked with 2 by 2 matrices whose entries are integers that exists in the line of the . This is witnessed due to the fact that how the subsequent points that are related to the integer E ( Q ), that seems to point of the E cover Q that seem to form of the abelian group. This is exactly where the premises of the is supposed to act.

The main idea that is needed to be noted here is that this is the Galois group and how it acts first on the basis of the modular curve which is the basis on which the modular form is going to be defined (Darmon and Merel, 1997). Hence the way interpretation of the Jacobean variety going to be witnessed (Darmon and Merel, 1997). The final thing that is needed to be noted is that how the that is the power order that is witnessed in the Jacobian (Adleman and Heath-Brown, 1985). The resulting representation in this case is not going to be 2 dimensional (Adleman and Heath-Brown, 1985). The main idea that is involved is that how the interplay between the mod 2 and mod 5 is being represented (Adleman and Heath-Brown, 1985).

Conclusion

Pierre De Fermat is known as one of the more influential mathematicians. Though he has done wealth of his work in the field of law, thing for which he is most well known is the last theorem (Adleman and Heath-Brown, 1985). The surprising thing about him is that during the course of his life, he published only one paper. The theorem was one of the greatest challenges for the ancient and the contemporary mathematicians. It was not until 350 years when the theorem was presented that its subsequent solution and proof was carried out by Wile’s (Adleman and Heath-Brown, 1985).

Works Cited

Adleman, L. M., and D. R. Heath-Brown. “The first case of Fermat’s last theorem.” Inventiones mathematicae 79.2 (1985): 409-416.

Brown, Tom C., and Allen R. Freedman. “The uniform density of sets of integers and Fermat’s Last Theorem.” CR Math. Rep. Acad. Sci. Canada 12 (1990): 1-6.

Cornell, Gary, Joseph H. Silverman, and Glenn Stevens, eds. Modular forms and Fermat’s last theorem. Springer Science & Business Media, 2013.

Darmon, Henri, and Loıc Merel. “Winding quotients and some variants of Fermat’s last theorem.” Journal fur die Reine und Angewandte Mathematik (1997): 81-100.

Darmon, Henri, Fred Diamond, and Richard Taylor. “Fermat’s last theorem.” Current developments in mathematics 1.1 (1995): 157.

de Fermat, Pierre. “Fermat’s Last Theorem.” 2001

GROOS, DYLAN, NATALIE SCHUDROWITZ, And KENNETH BERGLUND. “FERMAT’S LAST THEOREM.” (2016).

Jones, Gareth A., and J. Mary Jones. “Fermat’s Last Theorem.” Elementary Number Theory. Springer, London, 1998. 217-237.

Krantz, Steven G., and Harold R. Parks. “Fermat’s Last Theorem.” A Mathematical Odyssey. Springer, Boston, MA, 2014. 309-338.

Stewart, Ian, and David Tall. Algebraic number theory and Fermat’s last theorem. AK Peters/CRC Press, 2001.