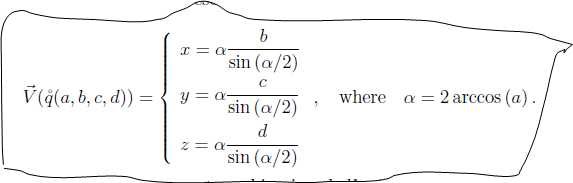Abstract
A discrete element method is a mathematical approach in which statistical measures of general characteristics or behavior of phenomenon are deducted from individual motions and interactions of an entity of elements. The research uses this methodology to demonstrate analyses of earth pressure against the retaining walls, including the quasi-static pressure of earth and lateral pressure of passive soil. Quasi-static analysis using Discrete Element Method on Yade Software is analysis for active and passive earth pressure distribution behind a retaining wall. Soil mass in a big container is treated as comprising blocks that associated to elastoplastic. Yade Methodology, i.e., discrete element method uses unbalanced ratio, damping ratio and inertial number as independent variables of simulated particles that are subject to time-step and P-wave velocity. Unbalanced ratio, damping ratio, and inertial dynamics equations are used based on the Classical Newtonian second law of motion. The forces and movements of each particle are traced and kept at every time-step. Contact forces rely on the particle geometry overlap and material compositions. The interaction force of each particle is included in the normal, tangential and moment components. Therefore, Discrete Element Method is the best method for analyses of soil structures, and the advantages using is this method are discussed.
Table of content Page number
1Introduction………………………………………………………………………………………………………………4
2Discrete element analysis ……………………………………………………………………………………………5
3Contructing a frame for Discrete Element Method………………………………………………………..6
4 Scientific simulations ………………………………………………………………………………………………..7
5Genration of a Discrete Element Method Sample…………………………………………….8
6DEM Formulation………………………………………………………………………………9
7Unbalance Force Ratio…………………………………………………………………………11
8Damping ratio…………………………………………………………………………………12
9Inertial number……………………………………………………………………………….12
10Quasi-Static……………………………………………………………………………………….12
11Time-step……………………………………………………………………………………13
12 P-wave velocity……………………………………………………………………………13
13Advantages and disadvantages of DEM……………………………………………………..14
14 conclusions ………………………………………………………………………………………………………………14
15References lists……………………………………………………………………………………………………….16
-
Introduction
Granular materials are normally found in natural materials as well as in different industrial aspects. Granular materials are conglomeration or collection of discrete or macroscopic particles associated with loss of energy as a result of particles interaction (Šmilauer and Chareyre, 2010). Thus, when granular materials interact there is a loss of energy. For instance, these materials can be found or are found in the extraction of mineral raw and transport, powder mixing, concrete, cereal storage, etc. Also, the granular materials are found in cohesive-frictional materials. Therefore, granular materials portray particular phenomena, which need more studies so to develop a better understanding of them. The elements can be deformed as macroscopic particles or solid bodies or soils, and they possess the ability to flow like liquids and compress like gases. Due to granular phenomena characteristics, numerical simulation method is being seen as the best method that could help understand the materials and as well predict their behaviour. Simulation has become a force to reckon with when it comes to optimization of industrial processes (Šmilauer and Chareyre, 2010). Therefore, the technological advancement on computing power is making the researchers use and implement numerical methods in experimental studies. Thus, simulation method helps researchers to use the deductive method in analysing the behaviour of granular materials. Hence, simulation method helps researchers to deduct a material characteristic from studying individual grain rather than studying as an entity.
Since the granular materials can be deformed as solid soils, they are highly discontinuous. Therefore, we should expect to use an intermittent simulation method to have a better understanding of these materials. Up to date, Discrete Element Method (Method) is the best approach in studying the granular materials behaviour. The discrete element analysis modelling is simple: the elements in the simulation are grains; they interact through pairwise contacts and are subject to external forces, i.e., gravitational force or interaction with surrounding objects (Šmilauer and Chareyre, 2010).
-
Discrete Element Analysis
A discrete element method is a mathematical approach in which statistical measures of general characteristics or behavior of phenomenon are deducted from individual motions and interactions of an entity of elements. Therefore, it uses deductive method, i.e., from specific to general. The discrete element analysis is mostly used where theoretical knowledge has no established mathematical equations. There different systems that exists that possess a certain phenomenon. For instance, there are gas systems, liquid systems, solid systems etc., but there those systems that are made of processes of the gas, liquid and solid systems like granular materials. Since these exists and we don’t have enough knowledge and a better understanding about them; thus, we develop a better research method to study them. Therefore, the best method to study these granular materials is introduction of efficient and effective simulation method to will help conduct experimental studies. There are different simulations methods that are used in engineering sciences today. They include: Discontinues Deformation Analysis (DDA), Finite Element Method (FEM) and the Discrete Element Method (DEM) (Šmilauer and Chareyre, 2010).
The best method to conduct our experimental studies is the Discrete Element Method. This method is best suited because it simulations is numerical and arithmetic in nature. The DEM method can indentify hard and soft particles. The numerical approach helps in establishing contact force of the granular materials. This method is the best in analyzing powder mixture, extraction of mineral raw and other related industries.
Due to granular phenomena characteristics, numerical simulation method is being seen as the best method that could help understand the materials and as well predict their behavior. Simulation has become a force to reckon with when it comes to optimization of industrial processes (Šmilauer and Chareyre, 2010). Therefore, the technological advancement on computing power is making the researchers use and implement numerical methods in experimental studies. Thus, simulation method helps researchers to use the deductive method in analyzing the behavior of granular materials.
Consequently, this discrete element method incorporates damping ratio in its numerical approach. The damping ratio measures the oscillatory behavior of the system when it’s disturbed way from their equilibrium level. For instance, when spring is pulled it bounces until it finds it equilibrium again. Also, the methods ensure that inertial number remains under 0.01%. Moreover, it ensures that unbalance force ratio remains within its desired range. The processes of settling the particle under gravity must be repeated several times to ensure that unbalance force ratio remains within its desired range. Furthermore, the method use time-step tool. The Time Step simulation tool enables you to particularly outline the operating conditions and acquire power flow solution for the limited amount of time. The time step provides the tools needed to evaluate the operation of the simulation systems by taking a specified amount of time.
The simulations are never in equilibrium status; thus, to make the equilibrium more balance the level of unbalanced force must be minimal as possible. Consequently, the level of inertial number must be at the less than 0.01%. Therefore, keeping these factors float and at their smallest level in their equation, will help in achieving static simulation. Therefore, the method establishes whether the simulations in equilibrium level.
Constructing a Frame for the Discrete Element Method
The aim selects a framework solution which can handle different simulation models. Therefore, the only model that can analyze the object-oriented abstractions is the analysis of the Discrete Element Method (DEM). Other models, i.e., Geometrical Model and Finite Element Method cannot be used to analyses the granular materials. The DEM method was first developed by Cundall with the aim to analyze rocks. Therefore, DEM method is a numerical approach that can illustrate the mechanical behavior or characteristic of an entity of discrete elements. The suitable interactions between the elements are noted to account for the mechanical compositions of the medium. Therefore, the macro-mechanical feedback of the granular material, i.e., deformability and strength is regenerated by establishing the micro-properties of the substance in contact interaction forces i.e. normal, tangential and local friction. The method sis is suitable since it gives new insight into collective modeling because the physical processes which dictate the collective behavior can be understood from a single grain. Discrete Elements constitute different geometries, but it keeps a low arithmetic calculation cost. The spherical containers are used, and it will be the same to our case. The purpose of using YADE, Discrete Element Method is to ensure a stable and constant environment for implementation of computational algorithms.
-
Scientific Simulations
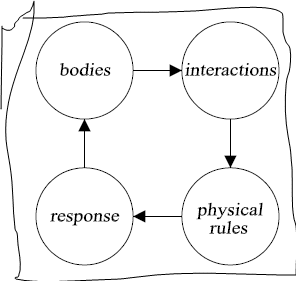
Taking into consideration that simulation involves bodies in which their interactions occur. The interactions are identified and processed to a particular level of computational algorithms and physical rules. The algorithms result in a moment, a force, etc., which it generates a response that influences the state of the body. Therefore, bodies and interactions assist in computational algorithms which are scientific simulations.
-
Generation of a Discrete Element Method Sample
There a different generation methods that be used to solve sphere in the three dimensions. The methods include the following. First, dynamic compaction, this method is used to raise the density of the soil higher when a particular subsurface disadvantages other methods functionality. Therefore, this method helps in increasing the density of the soil. Second, radius growth helps in solving geometrical equations for the sphere arrangement. The obtained arrangement has to posses the required porosity, and the sphere container should be small as possible. The sample is produced by assuming that spheres position randomly can overlap one another; thus, the sample is in a bigger volume that the target volume. After this is done the compression is done without friction and cohesion taking place, this done until the required stress of the walls is achieved. You can opt to use kinematic radius growth or dynamic compaction for the activity. The compression is done by using triaxial compression.
-
DEM Formulation
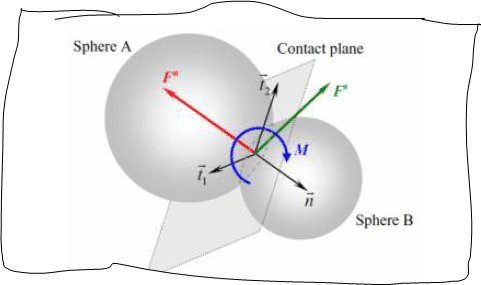
Let small container (S) and bigger container (B), be in contact. Therefore, the radius of the spherical element of small container is Rs and that of b to be rB. In general set of axes, their jurisdiction is interpreted by two vectors ~xS and ~xB. The interaction force can be represented by the element of S, and element of B; thus, these elements can be decomposed to shear vector.
The figure show the interaction between two discrete element smaller container (sphere b) and bigger container (sphere a).
The interaction moment is performed to ensure that representation of the missing particles in the spherical Discrete Element Method, the contact moment is determined by using the rolling stiffness Kr:
Thus, °At=c and °Bt=c are first orientations of the containers, taking into consideration the time contact was created.
Whereas, °At and °Bt are immediate orientations of spheres
Symbol° represents a quaternion
The ~V (•) function changes from quaternion form to a vector form:
Interpretation
The °q is a quaternion with these functions a, bi, cj and dk. Therefore, incase rotation angle α = 0 axes will become anything since the angle evolvement all zeros are assigned to x, z, and y function.
YADE is designed in such way that new simulation models are reused. Thus, the new simulations are easily defined.
-
Unbalanced Force Ratio
Unbalance force: the entity of particles under experimental studies settle in the bottom of the spherical containers due to gravity they bounce back. The processes of settling the particle under gravity must be repeated several times to ensure that unbalance force ratio remains within its desired range. The position for unbalancing force ratio is required to be less than 0.01.
Newton’s second law states the acceleration of the object is directly proportional to the size net force, in the same direction as the net and inversely proportional to the mass of the object. Therefore, until the unbalanced force ratio is below 0.01, then their experimental results become invalid.
-
Damping ratio
For the simulation to reach an equilibrium level, there is a need for damping ratio. Thus, damping ratio helps the DEM to maintain simulation at an equilibrium level. The damping ratio measures the oscillatory behavior of the system when it’s disturbed way from their equilibrium level. For instance, when spring is pulled it bounces until it finds it equilibrium again. Thus, bouncing is oscillatory behavior, and it is measured using a dimensionless measurement called damping ratio. Therefore, when conducting the experiment, we shall insert gravitational force until the particle settles in the bottom. Since our desired damping ratio is 0.02, the system parameter will be underdamped. Therefore, we will conduct the simulations by factoring in unbalance force and velocity to maintain particles at their equilibrium level.
-
Inertial Number
Inertial number ensures that the level of stress, density, and rate of the wall are within the desired range. The inertial number determines the types of static in simulations. Therefore, to keep the simulations in Quasi-static, the inertial number must be less than 0.0001.
-
Quasi-static
The simulations are never in equilibrium status; thus, to make the equilibrium more balance the level of unbalanced force must be minimal as possible. Consequently, the level of inertial number must be at the less than 0.01%. Therefore, keeping these factors float and at their smallest level in their equation, will help in achieving static simulations. The inertial number and unbalanced force ratio facilitate in achieving the quasi-static.
Time-Step
The Time Step simulation tool enables you to particularly outline the operating conditions and acquire power flow solution for the limited amount of time. The time step provides the tools needed to evaluate the operation of the simulation systems by taking a specified amount of time. Discrete Element Method has limited time in its simulations; thus, the time the simulations will take a specific amount of type. YADE duration of simulation is limited; thus, the time plays an important factor is simulations (Matsuzawa and Hazarika, 1996). The time step must be very small to understand how long one force does take to move one place to another.
-
P-wave Velocity
The P Wave is accumulation wave produced by the deforming front as it moves the atria. The right wave atrium depolarizes moment before the left atrium; thus, the speed the right atrium takes to travel to the light atrium is considered to be p-wave velocity. P-wave velocity: it is a direction compression wave; the p-wave velocity helps you in determining the time-step. The P-wave velocity is the speed that one force takes from moving one place to another. Therefore, determining time step, we calculate the distance the force have covered and note the p-wave velocity (Matsuzawa and Hazarika, 1996). Thus, we have distance and speed we can determine time step.
-
Advantages and Disadvantages of the Discrete Element Method
One of the advantages of the discrete element method is that it can be used in simulating a wide variety of granular materials and help in understanding better of rock mechanics condition. The researchers have on their own developed software that capable of simulating (Šmilauer and Chareyre, 2010). These simulations software are now adopted in experimental studies in a wide range of engineering applications. Therefore, discrete element method helps in studies of granular flow, extraction of mineral raw and adhesive powders.
Also, DEM method gives detailed research of the interactions of micro-dynamics of granular materials than physical experiments. Thus, the method gives a comprehensive and details experimental studies which help the researchers to understand granular materials.
Disadvantages of the DEM
The number of particles and duration of simulation is limited by the computing power. Thus, the method cannot simulate a lot of particles since the software requires a certain amount of particles with limited time to conduct the experimental study.
Discrete Element Method is numerical demanding, due to this factor the method has not been widely adopted in engineering sciences and related computational industries. However, the method has wide large computing core which is tedious. Also, the method is not energy efficient as CPUs.
-
Conclusion
In conclusion, the granular materials are normally found in natural materials as well as in different industrial aspects. These materials can be understood better through experimenting them using the Discrete Elements Method; since granular materials are conglomeration or collection of discrete or macroscopic particles associated with loss of energy as a result of particles interaction. Thus, when granular materials interact there is a loss of energy. For instance, these materials can be found or are found in the extraction of mineral raw and transport, powder mixing, concrete, cereal storage, etc. Also, the granular materials are found in cohesive-frictional materials. Therefore, granular materials portray particular phenomena, which need more studies so to develop a better understanding of them. The materials can be deformed as macroscopic particles or solid bodies or soils, and they possess the ability to flow like liquids and compress like gases. Due to granular phenomena characteristics, numerical simulation method is being seen as the best method that could help understand the materials and as well predict their behavior. Simulation has become a force to reckon with when it comes to optimisation of industrial processes. Therefore, the technological advancement on computing power is making the researchers use and implement numerical methods in experimental studies. Thus, simulation method helps researchers to use the deductive method in analysing the behaviour of the granular material (Kenmochi, And Yagi, 1978). A discrete element method is a mathematical approach in which statistical measures of general characteristics or behaviour of the phenomenon are deducted from individual motions and interactions of an entity of elements. Therefore, it uses deductive method, i.e., from specific to general. The discrete element analysis is mostly used where theoretical knowledge has no established mathematical equations. The Discrete Element Method is the most effective simulation method that can help us understand the phenomenon particles better. Unlike the other simulations the Discrete Element Method (DEM) uses mathematical approach to evaluate and analyses particles under study. The position for unbalancing force ratio is required to be less than 0.01 to make sure simulation is in static level. Similarly, the inertial number is supposed to below 0.01% to ensure simulation in order. Therefore, keeping these factors float and at their smallest level in their equation, will help in achieving static simulations. The inertial number and unbalanced force ratio facilitate in achieving the quasi-static.
References lists
Matsuzawa, H. and Hazarika, H., 1996. Analyses of active earth pressure against rigid retaining wall subjected to different modes of movement. Soils and Foundations, 36(3), pp.51-65.
Kenmochi, S. And Yagi, H., 1978. Experimental study on earth pressure of retaining wall by field tests. Soils and Foundations, 18(3), pp.27-41.
Fang, Y.S., and Ishibashi, I., 1986. Static earth pressures with various wall movements. Journal of Geotechnical Engineering, 112(3), pp.317-333.
Šmilauer, V. and Chareyre, B., 2010. Yade dem formulation. Yade Documentation.
Rankine, W.M., 1857. On the stability of loose earth. Philosophical Transactions of the Royal Society of London, pp.9-27.