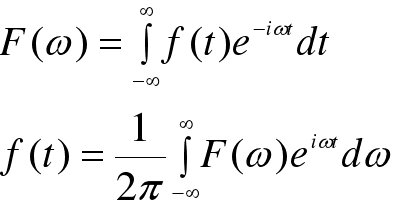Computer Aided Tomography

Introduction

Computer Aided Tomography (CAT) is a system for showing a portrayal of a cross-segment examination and imaging through the human body or any strong question utilizing X-rays and Ultrasound. It joins the normal X-rays with advanced computer flag handling to create an unrestricted image of the tissues of the body i.e. it keeps away from perusing the shadows of tissues while catching images of organs [3]. The underlying image is acquired in a simple frame, which is later changed over to a computerized shape utilizing an A/D converter. This computerized image is additionally sustained in computers for the reconstruction of images. Reconstructing of the images acquired from the sweep is done in a few stages with the assistance of an algorithm. This algorithm takes after the back projection technique and a channel to acquire clearer images. The tomographic framework developed with time [4]. A projection is a line vital to an object.

Back projection is a superposition technique and it entireties the information from the projection sees. Back projection uniformly appropriates the projection area information back similarly from which the line-integrals were shaped. The back-projection algorithm helped in getting better quality images, and this algorithm could be utilized for some different applications to acquire the complete structure of a body with its projected images accessible with the assistance of a sift, which would clear through all the obscuring components in an image [1]. In current frameworks, doctors can acquire quality images making it simple for them to consider the subject.

Background Mechanism

Given an arrangement of projection information, tomographic reconstruction takes into consideration the perception of cross segments of a protest in a non-intrusive manner. Different reconstruction strategies, estimation apparatuses and systems have been created and effectively connected to fields like prescription, cosmology, oceanography, industry and so on.

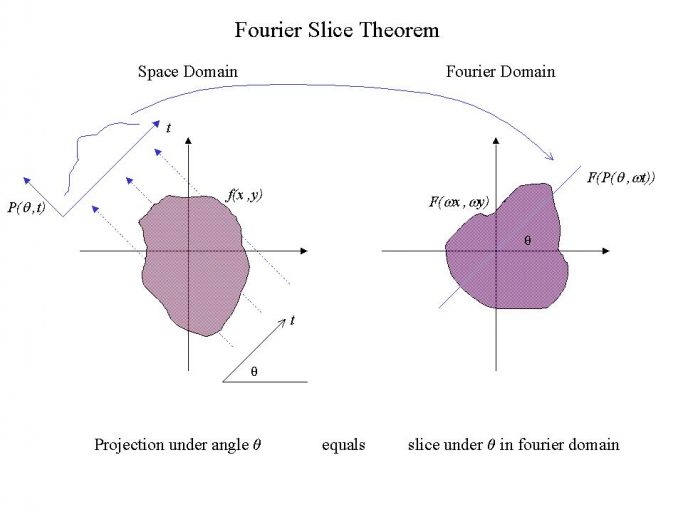
In spite of a few eccentricities because of the particular application, tomographic projection and reconstruction forms depend on a typical system in which Fourier theory, with the outstanding Fourier Slice Theorem (which expresses the connection between the Fourier Transformations of parallel projections and the 2D Fourier Transformations of the question cross-area), assumes a focal part [5].

In addition, an extraordinary class of reconstruction techniques, known as Direct Fourier (or Fourier-based) strategies, stems straightforwardly from this theory.

The initial Fourier-based reconstruction strategy (connected to space science) was depicted in 1956 by Bracewell [1]. From that point forward, numerous Fourier0based techniques have been produced, both for projection and reconstruction. With the utilization of the FFT (Fast Fourier Transform) algorithm, Fourier0based reconstruction strategies are the speediest now accessible, being favoured in information-intensive applications like microtomography [2], and reasonable for 3D reconstruction. Truth be told, compared with the Filtered Back projection FBP strategy, which has a computational complexity of R(QT), the computational complexity of the immediate Fourier strategies is about R(QS logQ). Additionally, likewise, from the point of perspective of image quality, coordinate Fourier techniques are presently ready to compete with strategies like separated back projection [6].

Back Projection

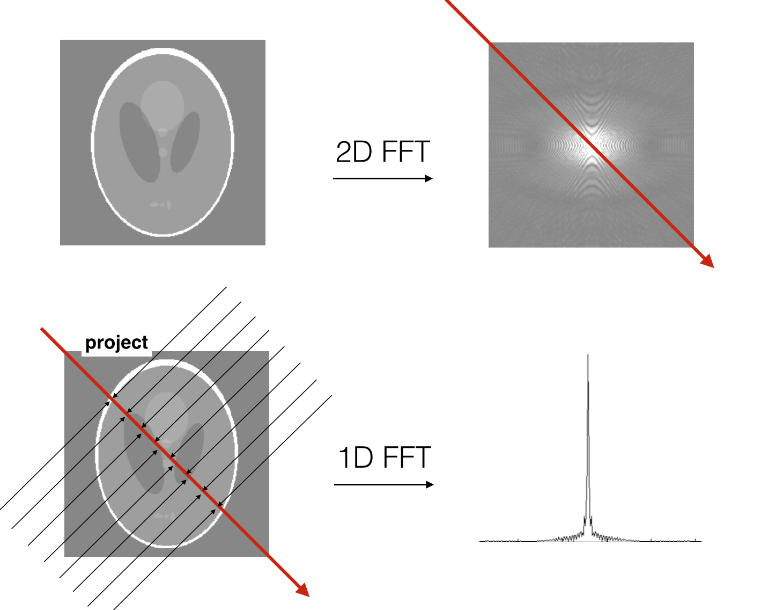
Back projection can be characterized as an imaging procedure that requires reconstruction from a few projections. It is an algorithm for especially ascertaining the commitment of each voxel in the structure. Backprojection is one of the most seasoned, productive and least difficult methods for reconstructing an image [7]. This image is considered as a test image for discovering its projected images and, after that, Backprojecting the images for the reconstruction of images. After each projection, the image begins getting clearer and increases the quantity of projections better images. Indeed, even after a few projections, the paper would understand that the test image that the paper acquired isn’t clear. With a specific end goal to expel all the obscuring components from the image, the paper makes utilization of a channel after each progression [8].

When the paper project the above outline from the most extreme conceivable cases, the paper observed that the image gets clearer. Images given beneath delineate the image acquired after a characterized number of projections. Soon after the principal projection, the paper scarcely discovers any lucidity in the image. In any case, as the number of projections builds, the image clearness improves [9].

Basic Functioning Of Tomography

Some physical wonders can be displayed, from a numerical point of view, as the estimation of a line integral of some physical parameter along straight lines. For example, in Computer Tomography (CT), the intensity of an x-beam going through a body endures a lessening that can be demonstrated as the integral of weakening coefficient of the tissues ascertained along the line from centre to an identifier.

The dispersion of a parameter on a transversal area of a question is portrayed by a 2D work in the plane of the segment. In a large portion of the applications (medicinal, for instance), the capacity I is restricted in space, which implies that it vanishes outside a limited locale of the plane. An imperative outcome of this trademark is that the 2D Fourier Transformations of a protest work aren’t band constrained.

Fourier Series Applications

Fourier Slice Theorem

The Fourier slice theorem expresses that:

Theorem: The Fourier Transformations of a parallel projection of a protest work i({> |) taken at a point gives a slice of the two-dimensional change of i({> |), I(x> y), subtending an edge with the x hub.

As it were, the 1D Fourier Transformations S() of the parallel projection s (v) gives the estimations of I(x> y) along line BB.

Fourier Reconstruction Methods For Parallel Projections

The Fourier slice theorem recommends a basic method to take care of the reconstruction issue. Taking parallel projections of the question work I at points R, S, q and Fourier, changing every one of them, the paper acquires the 2D Fourier Transformations of the protest work I(x> y) on q spiral lines. In perfect conditions (unbounded number of projections and tests per projection) I(x> y) would be known at all points in the frequency space, and the protest work i({> |) could be recouped by 2D reverse Fourier changing I(x> y).

Fourier reconstruction techniques (otherwise called coordinate Fourier or Fourier-based strategies) take after specifically from this perfect methodology, adjusted to the discrete case. By and by, just a limited number of projections and tests per projection are taken, and I(x> y) is known just on a limited number of points along a limited number of outspread lines and, so as to get a guess of i({> |) by 2D converse Fourier Transformations of I(x> y), the paper need to interpolate from the spiral points to the points on a Cartesian grid.

NUFFT based strategies

Some new algorithms have been proposed in light of late improvements associated with the proficient computation of discrete Fourier Transformations for non0equispaced information (NUFFT Non-Uniform Fast Fourier Transform [10]).

These algorithms are intended for various testing geometries in the Fourier area of the image and permit to play out the reconstruction completely, maintaining a strategic distance from the interpolation step. For example, in [11] and [12] the algorithm essentially streams in two stages: first, the 1D FFT of the projections is figured with a given oversampling factor getting a traditional oversampled polar grid, and afterwards, 2D reverse NUFFT is connected specifically to this example design.

Again in [13], another algorithm in view of the linogram geometry is portrayed. The algorithm streams precisely, with the distinction that, since the examples in the Fourier area are not equispaced in the vertical nor in the flat bearings, the 1D converse Fourier Transformations are performed through NUFFT rather than chirps change.

Fourier Series Method

In this technique, which utilizes traditional parallel projections and is depicted by [14], the interpolation in Fourier space is maintained at a strategic distance by relating (once more, in light of the slice theorem) the Fourier series of s (v) to the truncated Fourier series of the image work.

For this situation, a systematic equation for the correct assessment of the Fourier coefficients of i({> |) regarding the Fourier coefficients of s (v) is determined and executed with some estimate (a truncation of endless terms entireties). From the point of perspective of image quality, the consequences of this strategy are like those acquired with the sifted back projection technique.

Fourier Reconstruction Methods For Divergent Projections

Since the Fourier slice theorem applies just to parallel projections, the established Fourier reconstruction techniques don’t coordinate the instance of unique geometry. Figure 1 demonstrates a graphic portrayal of the Fourier slice theorem adjusted to dissimilar projections: the Fourier Transformations of a different projection taken at the edge gives, in the frequency space, q points along a curve.

Figure 1: Fourier Slice Theorem

Intuitively, one can imagine three conceivable approaches to applying Fourier reconstruction techniques to unique projections. The main path is to interpolate parallel projection information from unique projection information and afterwards essentially apply an established Fourier reconstruction strategy.

The interpolation procedure performed in the projections space is called rebinding and will be portrayed underneath. The second is to interpolate in the frequency area to a cartesian grid, and after that, 2D reverse Fourier Transformations like in established strategies (Figure 2).

Figure 2: Inverse Fourier Transformations

The latter is to build up a Fourier reconstruction strategy to be connected straightforwardly to the dissimilar informational index. As far as anyone is concerned, the second and the third way are still unattempted, likely because of the troubles in the interpolation step. In any case, exploiting late advancement in NUFFT figuring, an endeavour ought to be made with a specific end goal of backwards Fourier Transformations in view of such a cartesian plane.

Fourier Projection Method

The Coordinated Fourier technique can likewise be connected in the turnaround arrange to take into account the count of projection informational indexes from an advanced example protest.

2D Fourier transform (through FFT)

Cartesian to polar interpolation 1D discrete opposite Fourier transform (through FFT algorithm) of the spiral portions od the polar grid getting the parallel projections.

Notwithstanding the typical issues because of interpolation in the Fourier space, the Fourier projection strategy has been utilized as a part of iterative reconstruction strategies keeping in mind the end goal to accelerate the reprojection step [15].

Methodologies like those portrayed for the reconstruction techniques can be utilized as a part of the request to decrease the interpolation mistake.

As of late, Fessler has depicted another Fourier-based iterative technique utilizing min0max interpolation for the NUFFT, both in projection and in back projection steps, getting a productive iterative way to deal with the reconstruction issue [16].

Regardless, it must be pointed out that here the interpolation step isn’t so basic as in the reconstruction techniques since the example points in the beginning grid (Cartesian) are consistently conveyed.

The test system, both projection and reconstruction forms, has been executed in Matlab, and the reconstruction mistake has been quantitatively assessed, estimating the separation between the first and the reconstructed images. For this reason, the paper has utilized the separation measurements proposed by [17] (d0 standardized root mean squared separation, r0 standardized mean supreme separation, e0 most pessimistic scenario remove measure) connected to the locale of interest of the images.

Following are demonstrated a few images got with various reconstruction strategies connected on a similar parallel projection informational index and outlined the consequences of the reconstruction mistake assessment (Figure 3). At first look plainly the nature of the DFM with straightforward two-dimensional direct interpolation in the Fourier space is unsatisfactory; however, it altogether enhances introducing zero cushioning of the projections.

Figure 3: Reconstructed Images

Also, with the introduction of two-dimensional cubic interpolation in the Fourier space, a stunningly better outcome is acquired, comparable to the outcome got through FBP. The conduct of the distinctive strategies can be graphically assessed where the inclining profile of the reconstructed images and of the first one is compared. Likewise, for this situation, the great nature of the DFM with zero cushioning and cubic interpolation in the Fourier area is affirmed [18].

Conclusions

A long way from the objective of having completely secured the subject, the paper has given an outline of the primary points of Fourier reconstruction strategies. Various executions have been portrayed, and some essential perspectives have been pointed out. Points like iterative Fourier-based algorithms have been recently touched, and others like 3D Fourier reconstruction have been left for encouraging distributions [19].

The consequences of the performed re-enactments have been broken down subjectively and quantitatively, demonstrating that immediate Fourier reconstruction strategies are a substantial contrasting option to the usually utilized FBP algorithm with a surprising decrease in computation time [20].

References

1. Zhang YD, Wang SH, Liu G, Yang J. Computer-aided diagnosis of abnormal breasts in mammogram images by weighted-type fractional Fourier transform. Advances in Mechanical Engineering. 2016 Feb 24;8(2):1687814016634243.
2. Birkfellner, Wolfgang. Applied medical image processing: a basic course. CRC Press, 2015.
3. Firmino, Macedo, Antônio H. Morais, Roberto M. Mendoça, Marcel R. Dantas, Helio R. Hekis, and Ricardo Valentim. “Computer-aided detection system for lung cancer in computed tomography scans: review and future prospects.” Biomedical engineering online 13, no. 1 (2014): 41.
4. Tom, Manu, Vignesh Ramakrishnan, Christian van Oterendorp, and Thomas M. Deserno. “Automated detection of Schlemm’s canal in spectral-domain optical coherence tomography.” In Medical Imaging 2015: Computer-Aided Diagnosis, vol. 9414, p. 941430. International Society for Optics and Photonics, 2015.
5. Görgel, Pelin, Ahmet Sertbas, and Osman Nuri Uçan. “Computer‐aided classification of breast masses in mammogram images based on spherical wavelet transform and support vector machines.” Expert Systems 32, no. 1 (2015): 155-164.
6. Todd, Lori A., Mallika Ramanathan, Kathleen Mottus, Robert Katz, Ashley Dodson, and Gary Mihlan. “Measuring chemical emissions using open-path Fourier transform infrared (OP-FTIR) spectroscopy and computer-assisted tomography.” Atmospheric Environment 35, no. 11 (2001): 1937-1947.
7. Wyawahare, Medha V., Pradeep M. Patil, and Hemant K. Abhyankar. “Image registration techniques: an overview.” International Journal of Signal Processing, Image Processing and Pattern Recognition 2, no. 3 (2009): 11-28.
8. Banhart, John, ed. Advanced tomographic methods in materials research and engineering. Vol. 66. Oxford University Press, 2008.
9. Fourmont, Karsten. “Non-equispaced fast Fourier transforms with applications to tomography.” Journal of Fourier Analysis and Applications 9, no. 5 (2003): 431-450.
10. Matej, Samuel, Jeffrey A. Fessler, and Ivan G. Kazantsev. “Iterative tomographic image reconstruction using Fourier-based forward and back-projectors.” IEEE Transactions on medical imaging 23, no. 4 (2004): 401-412.
11. Zhang, Yudong, X. Yang, Carlo Cattani, Zhengchao Dong, T. Yuan, and L. Han. “Theory and Applications of Fractional Fourier Transform and its Variants.” Fundamenta Informaticae151, no. 1-4 (2017).
12. Zhu, Zuowei, Nabil Anwer, and Luc Mathieu. “Deviation modeling and shape transformation in design for additive manufacturing.” Procedia CIRP 60 (2017): 211-216.
13. Rogge, Seppe, Thijs Defraeye, Els Herremans, Pieter Verboven, and Bart M. Nicolaï. “A 3D contour based geometrical model generator for complex-shaped horticultural products.” Journal of Food Engineering 157 (2015): 24-32.
14. Abdolali, Fatemeh, Reza Aghaeizadeh Zoroofi, Yoshito Otake, and Yoshinobu Sato. “Automated classification of maxillofacial cysts in cone beam CT images using contourlet transformation and Spherical Harmonics.” Computer methods and programs in biomedicine 139 (2017): 197-207.
15. Kumar, Mohit, Ram Bilas Pachori, and U. Rajendra Acharya. “An efficient automated technique for CAD diagnosis using flexible analytic wavelet transform and entropy features extracted from HRV signals.” Expert Systems with Applications 63 (2016): 165-172.
16. Zulkoffli, Zuliani, and Elmi Abu Bakar. “Pose Estimation using 1D Fourier Transform and Euclidean Distance Matching of CAD Model and Inspected Model Part.” In IOP Conference Series: Materials Science and Engineering, vol. 114, no. 1, p. 012038. IOP Publishing, 2016.
17. Barkana, Buket D., and Inci Saricicek. “Classification of Breast Masses in Mammograms Using 2D Homomorphic Transform Features and Supervised Classifiers.” Journal of Medical Imaging and Health Informatics 7, no. 7 (2017): 1566-1571.
18. Lanczos, Cornelius. Discourse on Fourier series. Vol. 76. SIAM, 2016.
19. Baratchart, L., J. Leblond, E. A. Lima, and D. Ponomarev. “Magnetization moment recovery using Kelvin transformation and Fourier analysis.” In Journal of Physics: Conference Series, vol. 904, no. 1, p. 012011. IOP Publishing, 2017.
20. Toivanen, J. M., T. Tarvainen, J. M. J. Huttunen, T. Savolainen, A. Pulkkinen, H. R. B. Orlande, J. P. Kaipio, and V. Kolehmainen. “Thermal tomography utilizing truncated Fourier series approximation of the heat diffusion equation.” International Journal of Heat and Mass Transfer 108 (2017): 860-867.